
Solusi Persamaan Nirlanjar Menggunakan Metode Secant (Secant Method)
-
Pada artikel kali ini saya akan membahas mengenai materi yang ada pada Mata Kuliah Metode Numerik, materi yang akan saya bahas kali ini adalah Solusi Persamaan Nirlanjar Menggunakan Metode Secant (Secant Method). Sebelum ke pembahasan lebih dalam, lebih baiknya kita pahami apa saja yang ada pada materi yang akan saya bahas kali ini.
Dalam Metode Numerik, pencarian akar f(x) = 0 dilakukan secara lelaran (Iterasi). Secara umum semua motode itu dibagi menjadi dua golongan besar diantaranya:
Perhatikan gambar dibawah ini :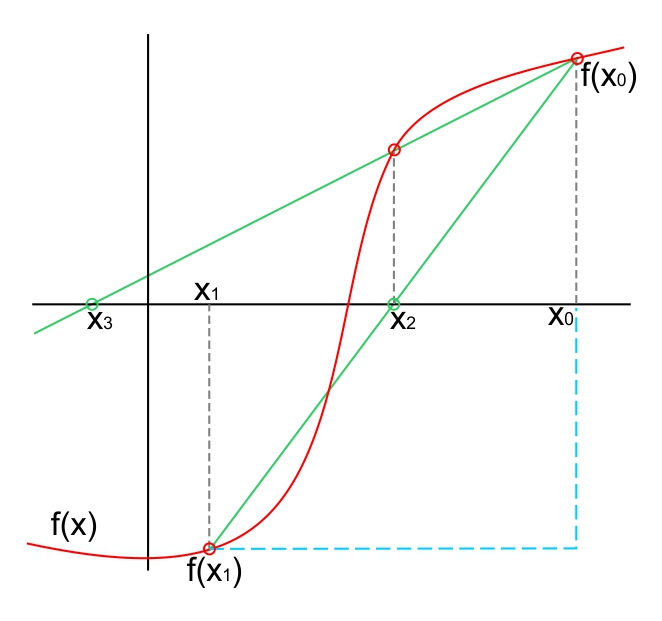 Persamaan garis l adalah
Persamaan garis l adalah
 Karena x = x2 maka y = 0, sehingga diperoleh
Karena x = x2 maka y = 0, sehingga diperoleh
 Secara umum rumus Metode Secant ini ditulis
Secara umum rumus Metode Secant ini ditulis
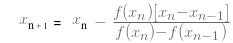
Prosedur Metode Secant :
Ambil dua titik awal, misal x0 dan x1. Ingat bahwa pengambilan titik awal tidak disyaratkan alias pengambilan secara sebarang. Setelah itu hitung x2 menggunakan rumus diatas. Kemudian pada iterasi selanjutnya ambil x1 dan x2 sebagai titik awal dan hitung x3. Kemudian ambil x2 dan x3 sebagai titik awal dan hitung x4. Begitu seterusnya sampai iterasi yang diingankan atau sampai mencapai error yang cukup kecil.
Contoh Soal :
Tentukan salah satu akar dari 4x3 – 15x2 + 17x – 6 = 0 menggunakan Metode Secant sampai 9 Iterasi.
Diketahui :
f(x) = 4x3 – 15x2 + 17x – 6
Penyelesaian :
Jadi salah satu akar dari 4x3 – 15x2 + 17x – 6 = 0 adalah 2
Sekian artikel Solusi Persamaan Nirlanjar Menggunakan Metode Secant (Secant Method), semoga bermanfaat, mohon maaf jika ada kesalahan. Jangan lupa Share juga artikel ini, sehingga teman-teman kamu dapat menerima informasi dari artikel ini dan jangan lupa juga untuk komentar mengenai artikel ini. Terima kasih~ XD
Dalam Metode Numerik, pencarian akar f(x) = 0 dilakukan secara lelaran (Iterasi). Secara umum semua motode itu dibagi menjadi dua golongan besar diantaranya:
- Metode Terbuka
- Metode Bagidua (Bisection)
- Metode Regulasi
- Metode Tertutup
- Metode Newton-Raphson
- Metode Secant
Perhatikan gambar dibawah ini :
 Persamaan garis l adalah
Persamaan garis l adalah
 Karena x = x2 maka y = 0, sehingga diperoleh
Karena x = x2 maka y = 0, sehingga diperoleh
 Secara umum rumus Metode Secant ini ditulis
Secara umum rumus Metode Secant ini ditulis
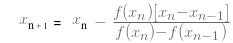
Prosedur Metode Secant :
Ambil dua titik awal, misal x0 dan x1. Ingat bahwa pengambilan titik awal tidak disyaratkan alias pengambilan secara sebarang. Setelah itu hitung x2 menggunakan rumus diatas. Kemudian pada iterasi selanjutnya ambil x1 dan x2 sebagai titik awal dan hitung x3. Kemudian ambil x2 dan x3 sebagai titik awal dan hitung x4. Begitu seterusnya sampai iterasi yang diingankan atau sampai mencapai error yang cukup kecil.
Contoh Soal :
Tentukan salah satu akar dari 4x3 – 15x2 + 17x – 6 = 0 menggunakan Metode Secant sampai 9 Iterasi.
Diketahui :
f(x) = 4x3 – 15x2 + 17x – 6
Penyelesaian :
- Iterasi 1 Ambil x0 = -1 dan x1 = 3 (ngambil titik awal ini sebarang saja, tidak ada syarat apapun)
- Iterasi 2 Ambil x1 = 3 dan x2 = 1.8
- Iterasi 3 Ambil x2 = 1.8 dan x3 = 1.84319
- Iterasi 4 Ambil x3 = 1.84319 dan x4 = 2.10932
- Iterasi 5 Ambil x4 = 2.10932 dan x5 = 1.96752
- Iterasi 6 Ambil x5 = 1.96752 dan x6 = 1.99423
- Iterasi 7 Ambil x6 = 1.99423 dan x7 = 2.00036
- Iterasi 8 Ambil x7 = 2.00036 dan x8 = 1.999996
- Iterasi 9 Ambil x8 = 1.999996 dan x9 = 2.00000
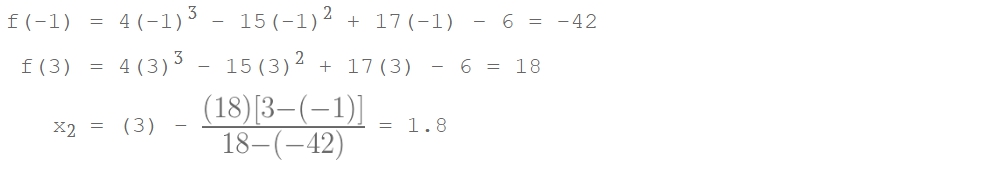
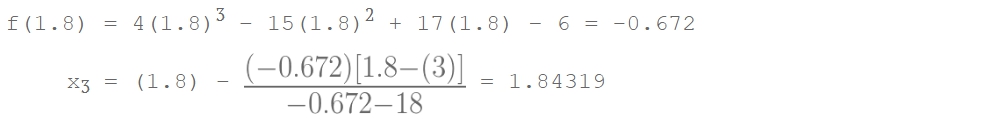

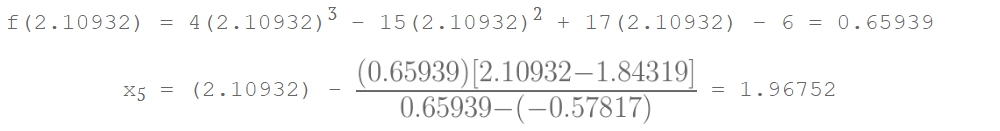




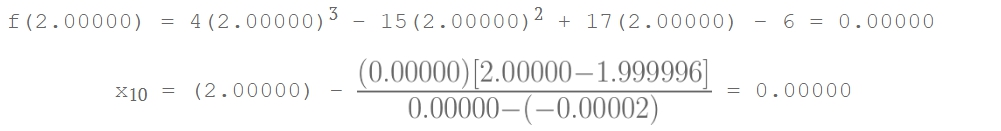
| n | xn-1 | xn | xn+1 | f(xn-1) | f(xn) | f(xn+1) |
|---|---|---|---|---|---|---|
| 1 | -1 | 3 | 1.8 | -42 | 18 | -0.672 |
| 2 | 3 | 1.8 | 1.84319 | 18 | -0.672 | -0.57817 | 3 | 1.8 | 1.84319 | 2.10932 | -0.672 | -0.57817 | 0.65939 | 4 | 1.84319 | 2.10932 | 1.96752 | -0.57817 | 0.6593 | -0.15303 | 5 | 2.10932 | 1.96752 | 1.99423 | 0.65939 | -0.15303 | -0.02854 | 6 | 1.96752 | 1.99423 | 2.00036 | -0.15303 | -0.02854 | 0.00178 | 7 | 1.99423 | 2.00036 | 2.00000 | -0.02854 | 0.00178 | -0.00002 | 8 | 2.00036 | 2.00000 | 2.00000 | 0.00178 | -0.00002 | 0.00000 | 9 | 2.00000 | 2.00000 | 2.00000 | -0.00002 | 0.00000 | 0.00000 |
Jadi salah satu akar dari 4x3 – 15x2 + 17x – 6 = 0 adalah 2
Sekian artikel Solusi Persamaan Nirlanjar Menggunakan Metode Secant (Secant Method), semoga bermanfaat, mohon maaf jika ada kesalahan. Jangan lupa Share juga artikel ini, sehingga teman-teman kamu dapat menerima informasi dari artikel ini dan jangan lupa juga untuk komentar mengenai artikel ini. Terima kasih~ XD

Kebijakan Berkomentar